Sorting algorithms are one of the most basic problems that modern computing had to deal with. That is why here I am going to present you one of the modern sorting algorithms implementation called
Library sort. This algorithm was presented at the
Third International Conference on FUN WITH ALGORITHMS as an improvement of the classic insertion sort algorithm, in which its implementation only runs on O(n log n) time.
In short, library sort works with an auxiliary array in which sorted elements will be inserted sequentially. This auxiliary array called S will however have gaps between the elements. These gaps are made out of empty elements (null in java objects, -1 in an array of indices, etc). The objective is to make place for new elements that, in their sorted position, should be located in the middle of previously inserted items. In the worst case, elements will be translated one place to the right or one place to the left in order to make place for that new item. Additionally, to insert elements as fast as possible, binary search will be used to locate an intermediate position where to put the next element.
Here we have a nice pseudocode:
Rebalance(Array S, Integer iniLen, Integer finLen)
k = finLen-1
step = finLen/iniLen
for j=iniLen-1 to 0:
S[k] = S[j]
S[j] = NONE
k = k-step
end for
LibrarySort(Array A, Integer n, Float epsilon, Array S)
goal = 1
pos = 0
sLen = (Integer)(1+epsilon)*n
while pos<n://For each round do this:
for i=1 to goal://Insert 'goal' elements to the sorted array S
//Search a position to insert A[pos]
insPos = binarySearch(A[pos], S, sLen)
if not IS_EMPTY(S[insPos]):
//Move elements to the right or the left in order to free insPos
freeSpace(insPos, S, sLen)
end if
S[insPos] = A[pos]//Insert new element
pos = pos + 1
if pos>n://All elements have been inserted
return LibrarySort
end if
end for
prevLen = sLen
sLen = min( (2+2*epsilon)*goal, (1+epsilon)*n )
//Rebalance array S
Rebalance(S, prevLen, sLen)
goal = goal * 2
end while
As a short complexity analysis we can state the following:
- There are
log2 n rounds
- In each round (n / log2 n) elements are inserted into the sorted array S in average.
- To insert an element it takes O (log2 n) time and a bit more because of binary search with intermediate gaps in between the array.
- At the end of each round, a rebalance is made that takes at most
(1+ε)n cycles, that means O(n) time.
- Conclusions:
- Total insertion time takes: O (log2 n * (n / log2 n) * log2 n) = O (n log n)
- Total rebalance time takes: O (log2 n * (1+ε) n) = O (n log n)
- Library sort takes O (n log n) time.
I have made my own C implementation of this algorithm that works as expected: no more than O (n log n) time.
#define MAX 10000
#define MAX2 20000
#define IS_EMPTY(e) (e<0)
#define NONE -1
void prepareLibrarySort(int epsilon, int n, int S[MAX2], int * sLen) {
int i;
*sLen = (1+epsilon)*n;
for(i=0;i<*sLen;i++) S[i] = NONE;
}
int searchFree(int e, int sorted[MAX2], int last) {
int first = 0;
int middle;
while(last>=0 && IS_EMPTY(sorted[last])) last --;
while(first<=last && IS_EMPTY(sorted[first])) first ++;
while(first<=last) {
middle = (first+last)/2;
if(IS_EMPTY(sorted[middle])) {
int tmp = middle + 1;
//Look to the right
while(tmp<last && IS_EMPTY(sorted[tmp])) tmp ++;
if(sorted[tmp]>e) {
tmp = middle - 1;
while(middle>first && IS_EMPTY(sorted[middle])) middle --;
//Look to the left
if(sorted[middle]<e)//Found intermediate position
return middle;
last = middle - 1;
} else first = tmp + 1;
} else if(sorted[middle]<e) {
first = middle + 1;
} else {
last = middle - 1;
}
}
//If no position was found return -1 or if a lower position was found, return that
if(last>=0 && IS_EMPTY(sorted[last])) last --;
return last;
}
void libSort(int A[MAX], int N, int S[MAX2], int EPSILON) {
if(N==0) return;
int j, k, step;
// ------ BASE CASE ------
//Goal: We want 'goal' elements to be inserted into S, for now..
int goal = 1;
//How many elements have already been inserted, its 1 for efficiency
int pos = 1;
S[0] = A[0];//We insert element 0 at position 0
//Initial size of array S
int sLen = max((1+EPSILON), goal + 1);
// ------ CONDITION -------
//What has already been read must be less than the total array size
while(pos<N) {
// ------ ROUND ------
//Each round i will end with goal=2^i sorted elements. i starts with 1
for(j=0;j<goal;j++) {
//Search where to insert A[pos] (with binary search)
int insPos = searchFree(A[pos], S, sLen-1);
//Because our binary search returns us the location of an smaller item than the one we search...
insPos ++;
if(!IS_EMPTY(S[insPos])) {//There is no place where we wanted to insert that element
int nextFree = insPos + 1;//Search a free space forward
while(!IS_EMPTY(S[nextFree])) nextFree ++;
//At 'nextFree' there is a place, translate all elements one position to the right
if(nextFree>=sLen) {//Wait! nextFree is out of bounds
insPos --;
if(!IS_EMPTY(S[insPos])) {
//Search backward
nextFree = insPos - 1;
while(!IS_EMPTY(S[nextFree])) nextFree --;
//Now we translate all the elements to the left
while(nextFree<insPos) {
S[nextFree] = S[nextFree+1];
nextFree ++;
}
}
} else {
//Now we translate all the elements to the right
while(nextFree>insPos) {
S[nextFree] = S[nextFree-1];
nextFree --;
}
}
//Now nextFree is insPos; in other words, insPos is free
} else if(insPos>=sLen) {//insPos is out of bounds
//Search a free space backwards
insPos --;//This place must be between the limits
int nextFree = insPos - 1;
while(!IS_EMPTY(S[nextFree])) nextFree --;
//Now we translate all the elements to the left
while(nextFree<insPos) {
S[nextFree] = S[nextFree+1];
nextFree ++;
}
//Now nextFree is insPos; in other words insPos is free
}
S[insPos] = A[pos ++];//We insert the element and increment our counter
if(pos>=N)
return;//That element was the last, return from the function
}
// ----- REBALANCE -----
//It takes linear time. Tries to spread the elements as much as possible
for(j=sLen-1, k=min(goal*(2+2*EPSILON), (1+EPSILON)*N)-1,
step=(k+1)/(j+1);j>=0;j--, k-=step) {
S[k] = S[j];
S[j] = NONE;
}
//In each round insert the double of elements to the sorted array
// because there will be the double of free spaces after the rebalance
sLen = min(goal*(2+2*EPSILON), N*(1+EPSILON));
goal <<= 1;//We increment i
}
}
void librarySort(int A[MAX], int n) {
int epsilon = 1;
int S[MAX2];
int sLen, i, j;
//This takes linear time
prepareLibrarySort(epsilon, n, S, &sLen);
//O (n log n)
libSort(A, n, S, epsilon);
//This takes linear time
for(i=0, j=0;i<sLen && j<n;i++)
if(!IS_EMPTY(S[i])) A[j++] = S[i];
}
In this example, I have used
ε=1 because after a few tests it was obvious that there will be no more efficient than that for this implementation.
| ε |
Time (ms) |
| 1 |
0.054474 |
| 2 |
0.094737 |
| 3 |
0.088421 |
| 4 |
0.131053 |
| 5 |
0.185922 |
| 6 |
0.213159 |
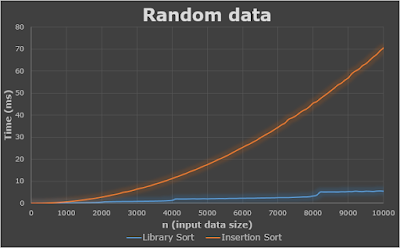
To compare efficiency between library sort and insertion sort, I made 2 tests. The first was a test with random numbers with n=[10, 10000]. The second one was the worst case scenario of both algorithms: numbers in reverse order. In the case of Library sort there is another as bad case as this one that is when the array is already sorted. Both are terrible for library sort. Here are the results:
Note that library sort generates a strange pattern. Every power of 2 input data size there is a cliff. The reason of that is because the sorted array size grows in a rate of a power of 2 (actually 2k+1-2). Then when the input data size is far to the left from a power of 2, the array S must have many empty spaces since it has just grown its size (check the goal variable). In that moment it is easier to insert data into the array.
In conclusion, there is no need to use insertion sort in most of the cases. Memory required for the implementation of library sort is O(3n). Unless the memory limitation is a very important factor, library sort will be the best solution.